공간정보와 인터넷지도

ComfyUI는 다재다능한 오픈소스 이미지 생성형 AI인 스테이블 디퓨전을 위한 GUI중 하나입니다. 원래는 AUTOMATIC1111이 훨씬 더 많이 사용되었지만, 여러가지 워크플로를 쉽게 생성하고 변경할 수 있어서 사용자가 급격하게 늘어나는 중입니다. 다만, ComfyUI는 스테이블 디퓨전의 기술적인 내용과 많은 관련이 있어서 사용하기가 쉽지 않습니다. 요즘 들어 ComfyUI 에 관한 글이 더 많아졌는데, 사용법이 잘 정리된 문서가 없어서 고민하던 중이었는데, 이 투토리얼은 아주 기초적인 내용부터 고급 사용법까지 아우르는 여러가지 내용을 담고 있습니다. 처음부터 따라해보면 ComfyUI를 좀 더 확실하게 이해하실 수 있게 될 것입니다. 이 투토리얼은 Open.ai 의 ComfyUI Academy 에 ..

이 글에서는 위와 같은 3d 캐릭터를 만드는 방법을 설명합니다. 위의 캐릭터는 제가 젊었던 시절의 사진을 아무거나 적당히 선택해서 생성한 것입니다 (원본보다 훨씬 낫습니다.ㅎㅎ) 사용한 워크플로는 이전 글과 거의 동일하며, 약간 수정만 했습니다. 그래서 글도 상당부분 중복되는 점 참고하시기 바랍니다. 소프트웨어 따라하기 다른 인물 테스트 요약 및 느낌 요약 및 느낌 소프트웨어 이 글에서는 스테이블 디퓨전용 GUI중에서도 제가 제일 좋아하는 ComfyUI를 사용합니다. ComfyUI가 처음이시라면, 설치 및 기본 사용방법 및 초보가이드를 확인하시기 바랍니다. 이 글에서는 IP-Adapter 중에서 FaceID Plus v2 모델을 사용합니다. FaceID 모델은 입력 이미지에서 얼굴을 추출하여 임베딩으로 ..

스테이블 디퓨전에서 어떤 특정한 인물의 얼굴을 넣으려면 LoRA를 학습시키거나 또는 dreambooth 를 사용해 checkpoint모델을 학습 시켜야 합니다.하지만, 새로운 모델을 학습시키는 것은 매우 시간이 걸리는 일입니다. 그런데, 이렇게 학습시킬 필요 없이 어떤 얼굴을 즉시 삽입할 수 있다면 어떨까요? 이 ComfyUI 워크플로는 입력 이미지로부터 어떤 인물의 얼굴을 복사합니다. 마치 맞춤형 LoRA나 체크포인트 모델처럼 사용할 수 있지만, 학습 시킬 필요는 없는 겁니다. 심지어는 매우 빠르고 편리합니다. 소프트웨어 따라하기 다른 인물 사용 실험 김태리 조인성 송혜교 테스트 결과 요약 소프트웨어 이 글에서는 스테이블 디퓨전용 GUI중에서도 빠르면서도 유연하여 사용자 저변을 급속히 확대하고 있는 C..

얼마전 스테이블 디퓨전을 사용해 판타지 바탕화면 월 페이퍼를 생성하는 방법을 알려드렸습니다. 3가지 스타일(중세/이집트/중국), 4가지 장소(마을/도시/궁전/성),4가지 계절(봄/여름/가을/겨울), 7가지 색깔 등을 조합해서 거의 무한정의 판타지 스타일의 바탕화면을 만들어주는 ComfyUI 워크플로입니다. 그런데, 한가지 아쉬운 점이 있었습니다. 요즘 모니터 가격도 싸졌고 그래픽 카드도 좋아져서 왠만하면 멀티 모니터를 사용할 수 있는데, 바탕화면 슬라이드 쇼 설정이 다중 모니터를 지원하지 않기 때문입니다. 즉, 윈도11 기본 바탕화면 설정만으로는 모든 바탕화면을 매번 동일하게 바꾸거나, 모니터별로 다른 바탕화면 이미지를 지정하는 방법이 불가능합니다. 저의 경우엔 모니터를 2개 사용하는데, 한쪽은 고정되어..

IP-adapter(Image Prompt adapter)는 이미지를 프롬프트로 사용할 수 있는 스테이블 디퓨전 애드온입니다. IP-adapter를 사용하면 참조 이미지로부터 스타일, 구도, 얼굴을 복사할 수 있습니다. 이 글에서는 IP-adapter의 여러가지 모델(Plus, Face ID, Face ID v2, Face ID portrait 등)과 이들 IP Adapter를 AUTOMATIC1111과 ComfyUI에서 사용하는 방법을 알아봅니다. 아래는 목차입니다. IP-adapter 모델 원래의 IP-adapter IP-adapter Plus IP-adapter Plus Face IP-adapter SDXL IP-adapter Plus SDXL IP-adapter Plus Face SDXL IP-a..

얼마전에 마이크로소프트 CoPilot에서 DALL-E 3 를 사용해본 글을 올렸습니다. DALL-E 3 는 특히 프롬프트를 이해하고 따르는 능력이 매우 좋다는 장점이 있고, 이미지를 수정하는 기능이 없고 크기를 변경할 수 없다는 점이 단점이 있다고 말씀드렸습니다. 하지만 Copilot에서는 무료로 사용할 수 있는 장점이 있죠. 이번에는 유료(한달에 20달러)인 ChatGPT 4에서 DALL-E 3를 테스트해보겠습니다. 제가 하는 일 때문에 한달간 유료 결재를 했거든요. 사실 ChatGPT 4를 계속 사용한다면야 한달 20달러가 그다지 비싸다고는 생각하지 않습니다. 하지만 개인적으로 사용하는 입장에서는 그냥 아깝죠. 테스트 방법은 예전 글에서 사용한 프롬프트를 재활용해서 비교하는 방식입니다. 그런데 제목 ..

스테이블 디퓨전을 사용해 인공지능 이미지를 생성할 때, 부정적 프롬프트를 사용하면 원하는 이미지를 얻을 확률을 높여줍니다. 사실은 부정적 프롬프트만으로도 이미지를 생성할 수 있습니다. 참고: 이 글은 부정적 프롬프트의 두가지 종류 중 하나입니다. 다른 하나는 부정적 이미지 프롬프트를 읽어보시기 바랍니다. 간단한 예 부정적 프롬프트의 원리 부정적 프롬프트가 없는 샘플링 부정적 프롬프트가 있는 샘플링 샘플링 공간(Sampling Space) 요약 간단한 예 긍정적 프롬프트만 사용할 경우 남자 이미지를 몇장 생성해 보겠습니다. 여기에서는 Stable Diffusion v1.5 모델을 사용합니다(사실 SDXL 쪽이 이미지 품질이 더 좋지만, 좀 성능이 떨어지는 모델로 생성해야 이 글의 목적을 달성할 수 있기 때..

무분류기 안내(CFG, Classifier Free Guidance) 척도(scale)은 스테이블 디퓨전 잡음 제거 샘플링 과정에서 프롬프트를 얼마나 잘 따를 것인지를 제어합니다. 이 값은 거의 모든 Stable Diffusion 기반의 인공지능 이미지 생성기에서 사용할 수 있습니다. 이제까지 제가 올린 글에는 CFG를 언급한 글이 매우 많은데, 이 글에서는 Stable Diffusion에서 CFG 척도가 무엇인지 좀 더 자세히 알아보겠습니다. CFG 척도가 하는 일 LCM과 turbo 모델의 CFG 척도 무분류기 안내란? 분류기 안내 무분류기 안내 무분류기 안내 척도 무분류기 안내의 학습 가장 좋은 CFG 척도는? CFG와 샘플링 단계의 관계 CFG를 납치하여 부정적 프롬프트 활성화 CFG 척도가 하는..

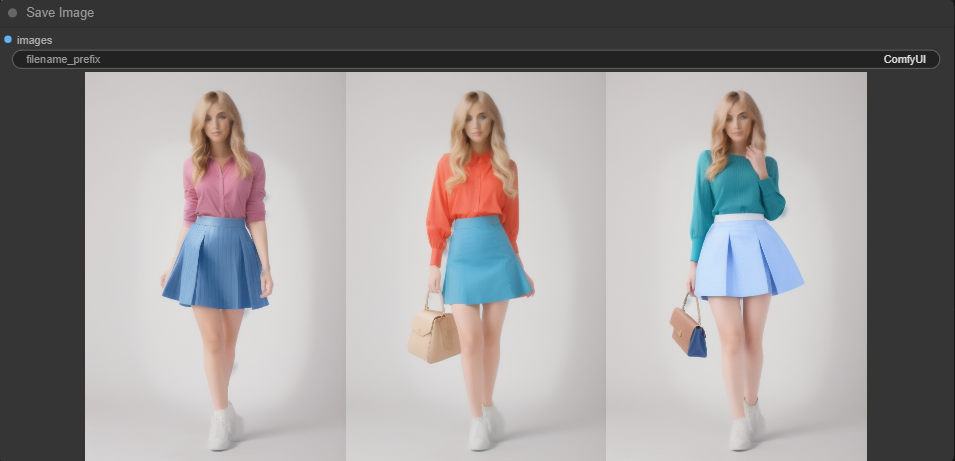
잡음제거 강도는 샘플링 단계에 들어가기 전, 이미지에 얼마나 많은 잡음을 추가할 것인지를 결정합니다. 특히 스테이블 디퓨전에서 image-to-image이지지 생성에서 공통적으로 사용되는 설정입니다. 잡음제거 강도는 0부터 1.0까지 설정할 수 있습니다. 0은 입력 이미지에 아무런 잡음을 추가하지 않는다는 뜻이고, 1.0은 입력된 이미지가 완전한 노이즈로 대체된다는 뜻입니다. 이러한 점에서 잡음제거 강도는 원 이미지를 보존하는 것과 완전히 새로운 이미지를 생성하는 것 사이의 균형이라고 생각하셔도 좋습니다. 결론적으로 잡음제거 강도를 높일 수록 이미지가 많이 변화하게 됩니다. AUTOMATIC1111에서 잡음제거 강도 image-to-image에서 잡음제거 강도 인페인트에서 잡음제거 강도 ComfyUI에서..

이 글은 animateDiff와 인페인트를 사용해서 일부분만 움직이는 이미지를 생성하는 ComfyUI에 대해 설명드립니다. 소프트웨어 따라하기 워크플로 설명 소프트웨어 이 글에서는 스테이블 디퓨전을 위한 GUI 중 하나인 ComfyUI를 사용합니다. 설치 및 기본 사용방법은 이 글을 보시면 됩니다. 조금 중복되는 부분도 있지만, 초보자 가이드도 참고하세요. 따라하기 0단계 : ComfyUI 워크플로 불러보기 아래의 그림을 다운로드 받고, ComfyUI 화면에 Drag&Drop하면 이 워크플로를 사용할 수 있습니다. 대부분 그냥 따라하면 그대로 사용할 수 있지만, 때때로 오류가 발생할 수 있습니다. 그러한 경우, 다음과 같은 작업이 필요할 수 있습니다. 처음 사용할 때 - ComfyUI Manager 를 ..

요즘은 그다지 컴퓨터 바탕 화면에 신경을 쓰지 않습니만, 한때는 고해상도 Wall paper를 구하느라 인터넷을 뒤적거렸던 기억이 나네요. 이 글에서는 여러가지 다양한 스타일의 바탕화면 이미지를 자동 생성해주는 ComfyUI 워크플로를 소개시켜 드립니다. 아래는 이 워크플로로 자동 생성한 월 페이퍼들입니다. 보시는 것처럼, 색깔/테마/계절 등이 다양하게 생성됩니다. 소프트웨어 따라하기 설정 변경 방법 Efficient 노드를 사용한 개선 버전 윈도11 바탕 화면 설정 윈도11 바탕 화면 설정 소프트웨어 이 글에서는 스테이블 디퓨전을 위한 GUI 중 하나인 ComfyUI를 사용합니다. 설치 및 기본 사용방법은 이 글을 보시면 됩니다. 조금 중복되는 부분도 있지만, 초보자 가이드도 참고하세요. 따라하기 1단..

임베딩(embedding) 혹은 텍스트 인버전(textual inversion)은 스테이블 디퓨전에서 이미지 스타일을 제어할 수 있는 또다른 방법입니다. 이 글에서는 임베딩이 무엇인지, 어디에서 받을 수 있는지, 어떻게 사용할 수 있는지 알아보겠습니다. 임베딩이란? 임베딩을 찾을 수 있는 곳 임베딩 사용 방법 유용한 임베딩 BadDream UnrealisticDream EasyNegative 추천 임베딩 wlop_style Kuvshinov 임베딩, 드림부스, 하이퍼네트워크의 차이 임베딩이란? 임베딩은 모델을 변경시키지 않고 새로운 키워드를 정의하는 방법인 텍스트 인버전의 결과입니다. 이 기법은 3~5개의 샘플 이미지 만으로 모델에 새로운 스타일이나 새로운 객체를 삽입할 수 있어서 주목을 받았습니다. 텍..

스테이블 디퓨전을 비롯한 많은 AI 이미지 생성기는 이미지를 프롬프트로 사용해서 비슷한 이미지를 생성하는 기능(이미지 프롬프트(image prompt)이 존재합니다. (AUTOMATIC1111에서는 이 글을 참고하세요) 일반적으로는 텍스트 프롬프트에 이미지에 추가하고자 하는 내용을, 부정적 프롬프트에 넣고 싶지 않은 내용을 지정합니다. 그런데, 이미지 프롬프트와 마찬가지로 이미지를 사용하여 내가 표현하고 싶지 않은 것을 지정하는 "부정적 이미지 프롬프트(negative image prompt)"가 있다면 어떨까요? 이 글에서는 스테이블 디퓨전에서 부정적 이미지 프롬프트를 구현하는 방법과, 재미있는 사례 몇 가지를 소개해 드립니다. 예를 들면, 아래 그림에서는 맨 왼쪽 사진에서 가운데 있는 잔디를 빼라고 ..

좋은 프롬프트를 만드는 과정은 모든 스테이블 디퓨전 사용자가 마주치는 첫번째 단계입니다. 이 글에서는 여러가지 실험과 사용자 들의 반응을 종합한 프롬프트 제작 절차 및 기법을 요약한 글입니다. 참고: 이 글을 읽고 실제 프롬프트를 작성할 때에는 chatGPT로 프롬프트를 만드는 방법도 추천드립니다. 아래는 이 글의 목차입니다. 좋은 프롬프트의 구성 피사체(Subject, 주제) 이미지 종류(Media) 스타일(Style) 예술 작품 공유 웹사이트(Art-sharing website) 해상도(Resolution) 추가 세부사항(Additional detail) 색(Color) 조명(Lighting) 부정적 프롬프트 키워드 목록 좋은 프롬프트를 만드는 절차 프롬프트 관련 기술적 사항 비슷한 얼굴 생성 방법 ..

Fooocus는 스테이블 디퓨전을 기반으로 한 무료, 오픈소스 AI 이미지 생성기입니다. Fooocus는 스테이블 디퓨전과 미디저니(Midjourney)의 장점을 결합하였습니다. 즉, 오픈소스, 오프라인, 무료로 사용할 수 있으며, 사용법이 매우 간단합니다. Fooocus는 스테이블 디퓨전 파이프라인을 최적화하여 고품질의 이미지를 생성합니다. 설정을 어떻게 바꿀까 고민할 필요가 없이, 그 시간에 어떤 이미지를 생성하고 싶은지를 고민하시면 됩니다. 아래는 이 글의 목차입니다. Fooocus의 장단점 Fooocus 설치 방법 Fooocus 사용 방법 고급 설정 성능(Performance) 설정 종횡비(Aspect Ratio) 설정 스타일(Style) 설정 모델(Model) 설정 이미지 확대(Upscale) ..